3x + 1 problem
Articles
Deterministic Structures in the Stopping Time Dynamics of the 3x+1 Problem (2026)
The Recursive Stopping Time Structure of the 3x + 1 Function (2018)
New Results on the Stopping Time Behavior of the Collatz 3x + 1 Function (2015)
On the Structure and the Behavior of Collatz 3n + 1 Sequences (2014)
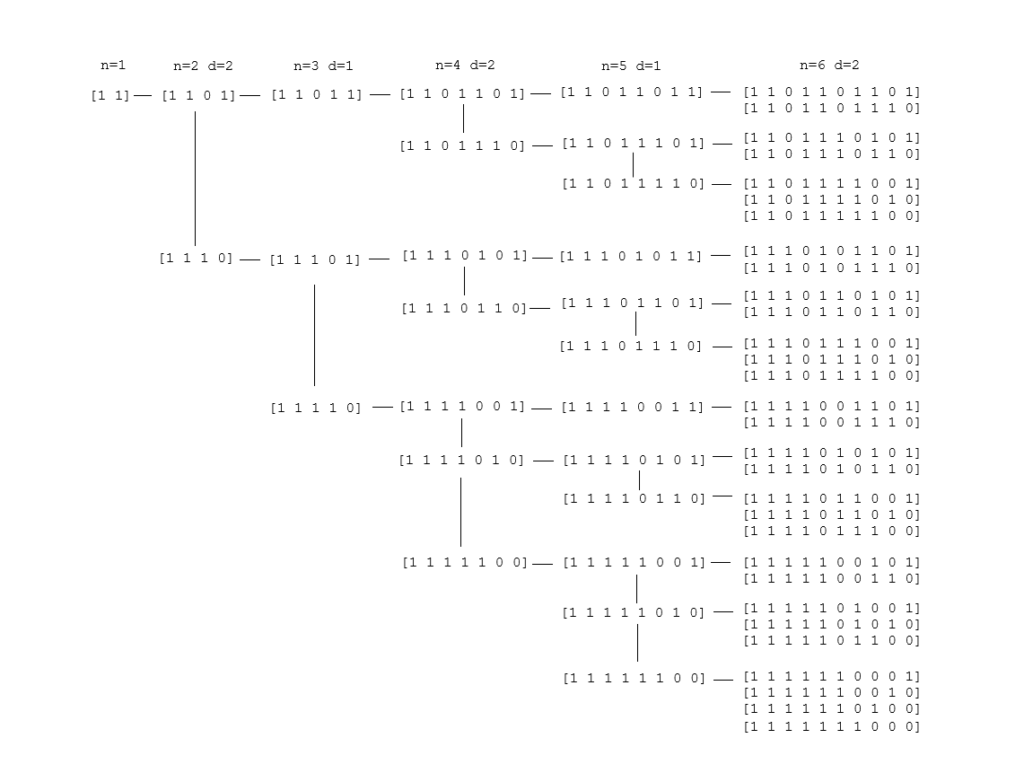
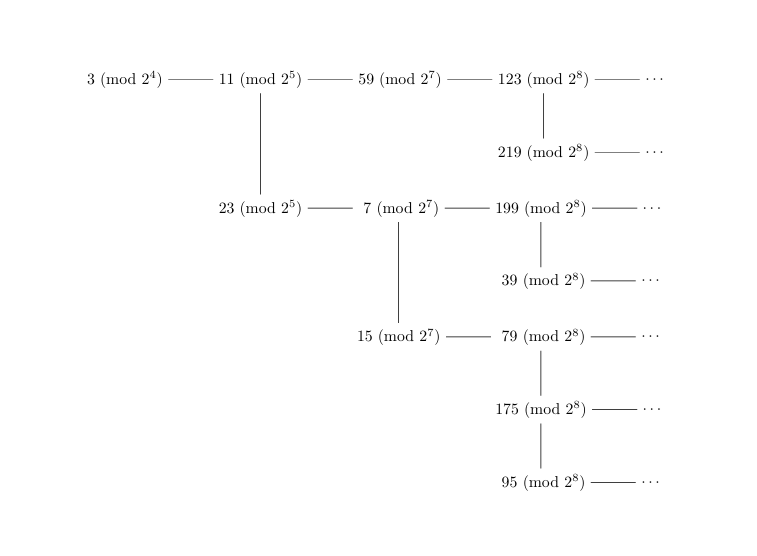
Die Konstruktion der speziellen Baumstruktur (2010)
Beobachtungen an einer speziellen Baumstruktur der ungeraden Collatz-Folge (2010)
Directed Collatz graphs
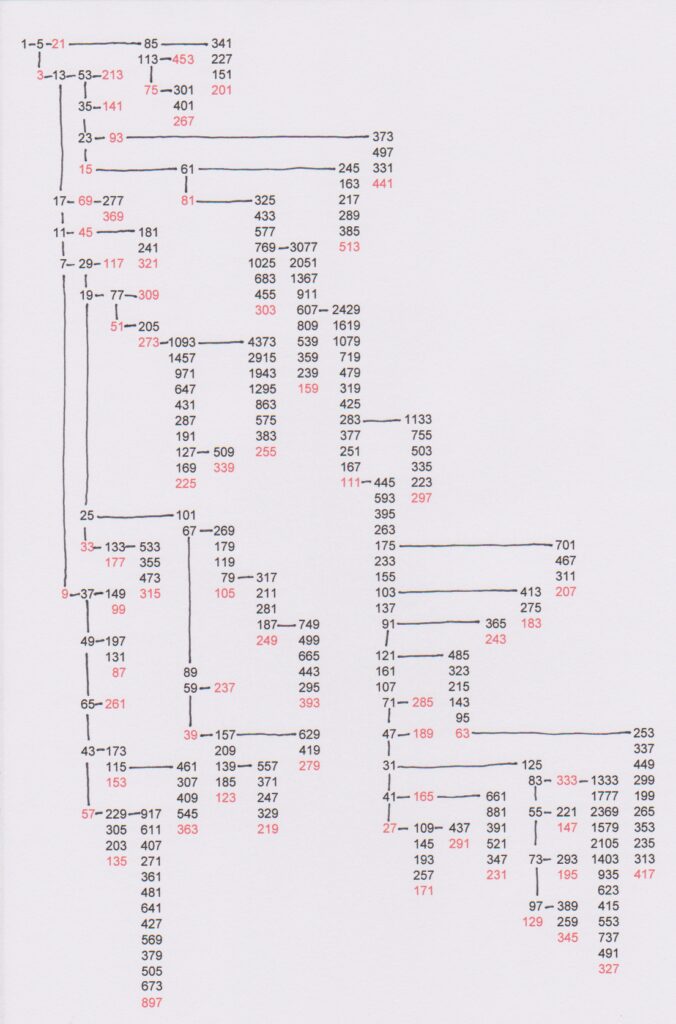
Conjecture: If we consider the distribution of numbers in this tree based on its first branches, a rough organizational structure can be observed. The leaves (red) of the first branches with the same number of columns form growth boundaries in the tree, which are closely related to the number of the main branch (1 – 5 – 21 – 85 – …) in the same column. The triangular structure of the tree provides the basis for this ordering principle: All odd numbers from 1 to a_n (a_4 = 341) can be found in the forwardings of the first branches up to the leaves 135, 267, and 201 in column S_4. The blue triangle illustrates the structure of this principle.
This ordering principle is fully valid up to column S_8 with a_8 = 87381. After this limit, either a very small error rate must be factored in, or the triangular scheme must be extended by one or more columns.
The following is a list of the first outliers. These are found starting with column S_9 with a_9 = 349525. The outliers are each smaller than the corresponding number of the main branch and are only found in the redirections of the next column.
S_9 (349525), Outliers: 300223, 263271, 316283, 210855
S_10 (1398101), Outliers: 843421, 1124561, 749707, 999609
S_11 (5592405), Outliers: 3998437, 5331249
S_12 (22369621), Outliers: 21324997
S_13 (89478485), Outliers: 20665775, 13777183, 18369577, 21324997
S_14 (357913941), Outliers: 336607519, 326201919, 299206683, 244651439, 217467945, 163100959